"Начало истории моделирования человеком окружающего мира скрывается в сумеречных далях седого палеолита..." Ленинградский геофизик

Начало истории моделирования человеком окружающего мира скрывается в сумеречных далях седого палеолита. На протяжении сотен тысяч лет люди жили собирательством, охотой и рыболовством, расписывая стены пещер рисунками. В позднем палеолите они пользуются не только огнем, но и колесом, гончарным кругом. Землю постепенно оставляют остатки последнего оледенения, на берегах плодородных рек в Египте и Месопотамии начинается копошение. Народы усиливаются, складываясь в крупные державы. Потребности государств в учете и контроле приводят к первым успехам, возникают причудливые, как мифы, арифметики, притягивающие к себе пришельцев издалека. Космогонические модели требуют тщательного ухода, питающего корни математики. Вначале слегка тронутое редкими мазками поселений, набирает вес Средиземноморье. К исходу бронзового века очаги старой культуры выгорели, центр событий перемещается на побережье Эгейского моря. В туманной дымке встречает утро Милет, самый южный из двенадцати городов Ионии на западной границе Малой Азии. Здесь живет Фалес, посетивший древние царства и набравшийся восточной премудрости. О его страстном увлечении астрономией знает каждый встречный и охотно расскажет вам о том, как чудак провалился в колодец, наблюдая звездное небо. Под полой походного плаща он принес на родину записи о таинственных египетских дробях, древние астрологические таблицы и желание постичь неизведанное. Фалес заслужил репутацию мудреца, предсказав солнечное затмение 585 г. до н. э.. Своей славой он пробудил в согражданах любопытство.

Будить любопытство греков - мероприятие, обреченное на повальный успех. Фалес скоро обзаводится последователями. Пифагор родился на острове Самос близ Милета и в своих путешествиях исходил немало дорог. Он познакомился с астрономией стран Востока. Его воображение поражает то, что для предсказания небесных явлений не надо задирать голову вверх. В числах Пифагор видит проводников в параллельный мир, показывающий внутреннее обустройство Вселенной. За ним не следят хранители, ревниво оберегающие сокровища знаний. Пифагор открывает число как загадочную шкатулку, трепеща и предвкушая увидеть чудо. В интуиции кладоискателя ему не откажешь. Задолго до изобретения комплексной арифметики, он наделяет число свойством отражать не только количественные, но и пространственные отношения предметов, появляется, например, треугольное число и прочие странные числа.

Пифагорейцев винят в мистицизме, но они не большие мистики, чем наши современники, додумавшиеся до относительности одновременности. В кружении вокруг треугольной фигуры Пифагор верен своей путеводной звезде. И она его не подвела, он стал самым известным математиком со времен сотворения мира. Прямоугольный треугольник это уже не прямая, но еще далеко не плоскость. При аппроксимации гипотенузы ступенчатой линией (лесенкой) ее длина упорно равна сумме двух катетов. Так как такое приближение не выдерживает проверки, ученый изобрел иной ход мысли, приводящий к результату, превосходно согласующемуся с опытом. В наши дни к его способу измерять длины по площадям приклеилась поговорка: "Пифагоровы штаны на все стороны равны". Если задуматься, чем ломаная линия отличается от прямой, помимо флюидно исчезающих при стремлении числа ступеней к бесконечности узлов, не следует ли сделать вывод о том, что умом постигаемых Вселенных существует несколько?

Полагая, что проводники в неведомый мир не должны путаться на дорогах и врать, Пифагор предпочел уйти от, безусловно, неприятного ему рассуждения. Возможно, он вовремя увидел и оборотную сторону медали, поскольку дискуссия вокруг знаменитой аксиомы Евклида о параллельных закончилась для профессора Лобачевского обвинением в помешательстве. Чернышевский в своих письмах издалека сурово осудил почтенного геометра, не простив ему сущей шалости - невинного предположения о том, что через точку на плоскости можно провести несколько прямых линий, параллельных некоторой обособленной прямой.

Зенон из Элеи, тот вовсе не стал помогать плутающему в потемках сознанию, а решительно подставил ему бойцовскую подножку. Совершенствуясь, как античный полубог, в логических построениях, он всякому желающему охотно доказывал, что окружающий нас мир не более чем обман зрения. Для того, чтобы и пастуху стали ясны его доводы, он оформил свои апории в похожие на басни высказывания, известные под названиями Ахиллес, Дихотомия (деление на два), Стрела и Стадион. Приведем первые две истории, пересказав их своими словами. Ахиллес. Ахиллес - самый быстроногий герой Илиады Гомера. Но и он не в состоянии догнать черепахи. В самом деле, когда скороход достигнет места, в котором черепаха была, она отползет на некоторое расстояние. И так будет повторяться без конца. Дихотомия. Допустим, что путник хочет пройти некоторое расстояние. Он должен сначала достичь половины пути. Каждая часть пути допускает, в свою очередь, деление пополам, и так до бесконечности, так что движение никогда не сможет начаться. Попробуйте отложить бесконечное количество поклонов и задайте себе вопрос, когда все это закончится? Никогда, подтвердите вы, ибо в этом состоит суть невыполнимости мероприятия. Аргументы Зенона показали, что доводы разума способны приводить к выводам, диаметрально противоположным наблюдаемым явлениям. Истории свойственно повторяться. На пороге двадцатого века физики уверяли всех, что ничто не способно смутить гармонии нарисованной ими картины мира, пока не получили удар из собственного лагеря. Нашлись отщепенцы, которые заявили, что возраст человека во Вселенной, как и всякой мелкой сошки в ней, зависит от позиции наблюдателя. Самое обидное, что, несмотря на явную бессмыслицу утверждения, будто бы Павел Павлович, сойдя с электрички, найдет своих закадычных приятелей более постаревшими, чем он сам, солидные книги сошлись вдруг во мнении, что так оно и есть на самом деле.

Но, если само время фикция, то в чем виноват Зенон? Он доказывал, что на изменения нужно смотреть философски, и неважно, что его коллеги, урезонивая мастера, молча ходили перед ним. Им было невдомек, что есть таки во Вселенной углы, из которых они видны как застывшие соляные столбики. Позвольте после этого не цитировать Аристотеля, который распял беднягу Зенона за то, что тот не оставил для слушателей пифагорейской лазейки: надо, дескать, оперировать скоростями, а не путями. Пусть этим пользуются школьники. Умозрительная теория в ловких руках оказалась инструментом более опасным, чем бритва. Изворотливые греки попытались найти рецепт лечения заблуждений ума, сложив миф о Гордиевом узле.

Согласно легенде, Александр Македонский, прохаживаясь по ярмарке, заметил зевак, столпившихся около телег, скрепленных намертво хитрым узлом. Желающие развязать узел отходили сконфуженно. Некий злонамеренный Гордий зарабатывал деньги на ставках, конечно, не совсем честно. Александр ударом меча рассек Гордиев клубок пополам.

У этого мифа и апорий Зенона есть общая часть, касающаяся спорной неразрешимости задачи. Если базироваться на предположении, что Гордий был проходимцем, зарабатывающим на хлеб внешним подобием морского узла, тогда Александр выглядит единственно мудрым в толпе человеком. Работа рассудка его оппонентов не вызывает нареканий, просто их действия изначально неправильно мотивированы. Урок, преподнесенный Зеноном, не прошел зря. После него ученые стали тщательно проверять исходные предпосылки. Особенно досталось всеми ругаемой бесконечности. Однако Евклиду не удалось изгнать ее окончательно из аксиом, на которых построено здание классической геометрии. Неопределенность, присущая и миру, оказалась платой за вход в него.

УКРУПНЕННАЯ ПАНОРАМА СОБЫТИЙ

Странное, что проступает при ознакомлении с хронометражем Земли, состоит в том, что в ее громадном по протяженности прошлом с легкостью могло бы уместиться множество цивилизаций, подобных нашей. Двести пятьдесят миллионов лет длится господство динозавров. В некоторых своих чертах они должны были достичь немыслимого совершенства. Кроме того, почва обязана быть нашпигована их останками. Неутомимый Фридрих фон Уене искал динозавров от Америки до Африки, а нашел кости чудовищного зверя в 48 километрах от места своего рождения в Тюбингене (Германия). Не путайте замерзших в Сибири мамонтов с древними монстрами. Динозавры вымерли шестьдесят миллионов лет тому назад, причины их ухода неясны. Последнее оледенение законсервировало животных каменного века, который отстоит от нас недалеко - рукой подать.

Учение Вернадского об оболочках Земли придает особое хирургическое значение сфере космического холода для формирования живого. Он пишет о направляемом холодом движении вещества, струившемся в косной материи задолго до появления первой белковой молекулы. В живой материи процессы идут в масштабе исторического времени, в косной - в масштабе геологического времени, "секунда" которого много больше декамириады, т.е. ста тысяч лет исторического времени. Биогенный ток атомов выковал человека. Примерно двадцать тысяч лет тому назад криосфера утянула щупальца ввысь, к заоблачным вершинам гор, ледяные реки обмелели, и началось победное шествие новоиспеченного существа. Болотистые низины, леса и пустыни заселили животные. Питаясь ими, "мыслящий тростник", как называл человека Паскаль, необычайно размножился. Он сумел справиться с легкоплавкими металлами, делал горшки, варил пиво. За этими достойными занятиями мы застаем его в неолите.

Великие реки - Нил, Тигр, Инд, позже - Ганг, Хуанхэ, а позже - Янцзы, приютили на пышных берегах сторонников интенсивного земледелия. Регулирование разливов и осушение болот повысило уровень жизни, что немедленно принесло плоды. Зародилась городская аристократия во главе с могущественными вождями. В раздорах и войнах возникли первые деспотии, объединившие обширные территории под властью единого монарха. Эту картину мы видим в Египте, Месопотамии, позднее в Китае и Индии. Стабильная сытая жизнь имеет свои недостатки. Благодаря устоявшейся традиции знания легко превращались в религии, передаваемые добросовестными учителями. В таком замороженном состоянии древние государства легко преодолевали тысячелетия. Чтобы стронуть маховик истории с места, на ее авансцене должны были появиться новые народы.

Средиземноморский бассейн по праву именуется местом рождения современной цивилизации. Три тысячи лет тому назад он был освоен финикийскими мореходами, связавшими ниточками торговых путей прибережные города. Этот образ напоминает мозг, окутанный кровеносными сосудами. Как орган мысли он и начал функционировать, подарив миру золотой век науки и искусства. Древние государства на Ближнем Востоке послужили щитом, оградившим его от напора кочевников. Омолаживающиеся царства сами время от времени пытались прибрать к рукам приморские территории. В борьбе Персия не смогла переломить хребет свободолюбивой Греции. Александр Македонский выполнил миссию, уготованную ему инерцией спора Востока и Запада. Он умер в покоренном им Вавилоне в 323 г. до н. э.. Античная история распалась на периоды до и после него.

До Александра наука питалась наставлениями бродячих проповедников мудрости. После него его полководцы поделили между собой богатства разросшегося эллинского мира. Сирия и Македония приглянулись Селевку и Антигону, затем только лишь, чтобы впоследствии достаться Риму. Потомки Птолемея превратились в фараонов. Благодаря их религиозной терпимости, им на триста лет подчинился Египет. Александрия прославилась как жемчужина в ореоле городов Средиземного моря. Образованные эллины, желая придать блеск новому центру Ойкумены, превратили науку в профессию. Римляне не трогали этот оазис, поскольку он не задевал их солдафонских амбиций, а наиболее просвещенные императоры черпали отсюда свое вдохновение. Цезарь снова возложил к ногам Клеопатры, дочери Птолемея XII, покоренный его солдатами город.

В Египте сошлись встречные традиции созерцать и размышлять, в итоге работы александрийских астрономов намного опередили свое время. Библиотека Александрии стала плацдармом для накопления знаний. Здесь были изданы "Начала" Евклида. Наше школьное образование в области геометрии почти целиком основывается на первых шести томах его сочинений. Арабы, захватившие в 630 г. Александрию, по сути, спасли некоторые труды от забвения. До них ценную библиотеку частично разграбили, частично сожгли захиревшие потомки бывших ее обладателей. Восточные ученые перевели уцелевшие книги, в таком виде работы древних мыслителей пережили долгие смутные времена.

На протяжении нескольких столетий в булькающем котле Европы растворились остатки рабовладельческого строя, как щелочь, разложившего античный мир. В мучительных поисках сложилась экономическая система нового типа, феодальные государства окрепли и, наконец, смогли обратиться к культуре. Накопленное античным миром богатство вернулось при полном своем блеске во времена Ренессанса.

Первыми абстрактными моделями действительности стали числа, в обозначениях цифр и оснований (11 на деле проще выразить как 10 и 1) люди проявили немалую изобретательность. Для распространенных оснований, кратных, очевидно, количеству пальцев на руках, а при большом торге, - еще и на ногах, стали возникать памятные знаки в виде пучков травы, зарубок на палках, узлов на веревках или ракушек, сложенных по пяти в кучки. Отсюда один шаг до возникновения специальных символов для пяти, десяти и т. д. Египетская десятка копировала сноп.

Римляне перевернули сноп, заострили угол и превратили в пятерку V. Резон приблизить основание к началу у них был простой, цифры от 1 до 9 простодушные египтяне отображали палочками. Экономные греки избрали в качестве цифр первые буквы своего алфавита. Древнеславянский счет заимствовал у греков эту идею. Рядом с цифрой, чтобы отличить ее от буквы, ставились разные знаки: черточки, кружочки. Забавное число "ворон" было окружено крестиками, как бы летающими птицами. Покорение континентов раскрыло сходную картину у других народов. В американском племени Майя цифры изображались точками, а основания черточками. Черточка обозначала пятерку. Размер полочки позволял выстроить над основанием несколько точек подряд:

. . .

= VIII = 8

Свои числа майя могли мастерить из ближайших предметов: камешков, щепочек. Цифры сходны с римскими, но это таинственное государство индейцев не знало колеса и затерялось в джунглях X века.

Повсюду в числовых системах древности мы видим удобство для выражения количественных отношений предметов. Делить добро собственник предпочитал скорее физически, нежели умственно. Попробуйте, допустим, хотя бы умножить MCXI на XVII. В Египте писцам ставились памятники. Размышления над несовершенством числа заставило Архимеда написать трактат "Исчисление песчинок".

В Китае первый царь, основавший династию Цинь, появился в 221 г. до н. э. Император приказал ввести для объединенных царской властью разноязычных племен символы не только для цифр, но и для слов. В наследство мы получили как бы незамкнутый алфавит, в котором изучению смысла одного знака можно было посвятить целую жизнь. Понятно, какие блестящие перспективы открывало это для учителей мудрости, чьи знания, умещающиеся в несколько иероглифов, способны были годами удерживать при себе толпы прилежных учеников

КОСМОГОНИЧЕСКИЕ МОДЕЛИ

В александрийский период изучению географии и астрономии посвятили себя Эратосфен, Аполлоний, Аристарх, Гиппарх, Птоломей и десятки других светил эллинской науки. Все это способствовало тому, что александрийцы создали астрономическую теорию, которая на протяжении пятнадцати столетий оставалась непревзойденной.

Эратосфен (родился примерно в 276 г. до н. э.) известен тем, что измерил радиус Земли, заглянув в колодец.

В день летнего солнцестояния в Сиене, ныне Асуан, в полдень солнечные лучи освещали дно глубокого вертикального колодца, в то время как в Александрии стержень солнечных часов отбрасывал в полдень короткую тень. Сопоставив эти два факта, ученый решил подкрепить свои догадки относительно формы Земли вычислениями. Предположим, что солнечные лучи в Александрии и Сиене практически параллельны. Перед нами фигура, которая предстала мысленному взору Эратосфена:

Фигура, которая предстала мысленному взору Эратосфена

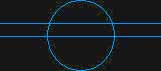
Сиена отстоит от столицы на 5000 стадий, будучи примерно на том же меридиане. Тщательно юстированные солнечные часы позволяют по тени стержня измерить главное, что нужно геометру, - угол между солнечным лучом и земной поверхностью в Александрии. Решив геометрическую задачу, Эратосфен показал, что расстояние между городами, отложенное по поверхности земного шара, должно составлять 1/50 окружности Земли. Отсюда он нашел длину окружности Земли равной 250 000 стадий, что соответствует приблизительно 39 690 км.

В теории чисел известно "решето Эратосфена". Сначала берется крупное решето, через него выпадает все, что делится на два. Затем более мелкое отсеивает все, что делится на три, и т. д. Сухой остаток - простые числа, делятся только сами на себя. Блестяще образованный даже для грека ученый, не довольствуясь успехами в математике, астрономии и географии, выступал также на поприще поэзии, истории, грамматики и литературной критики и был удостоен почетного прозвища "Бета" (по названию второй буквы греческого алфавита) за то, что во всех этих областях знания уступал лишь сильнейшим.

Аристарх Самосский (родился в 310 г. до н. э.) вычислил расстояния до Луны и Солнца следующим занятным образом.

Астроном наблюдает восход Луны и определяет угол между направлениями на нее и на некоторую неподвижную звезду. Положение далекой звезды не зависит от вращения Земли. Другое дело, более близкий к нам спутник, уже через 12 часов наблюдатель фиксирует его на новом месте. Этого вполне достаточно для расчета расстояния до Луны, Аристарх нашел его равным 56 радиусам Земли (действительное - 60,2 радиуса Земли). Оценивая расстояние до Солнца, астроном определяет угол между направлениями на него и на Луну в тот момент, когда спутник Земли находится в квадратуре, т.е. видна четверть Луны. Тогда космические тела расположены строго по углам прямоугольного треугольника, о котором теперь многое что известно. Оружием Аристарха был великолепный труд Евклида, написанный несколькими десятилетиями ранее.

Евклид занимался, собственно, оптикой. С его подачи в совершенных солнечных лучах геометры видят прямые линии.

Сплотивший ученых Египет располагал колоссальными сведениями о движениях планет. Находки Аристарха Самосского не помогли устоять гелиоцентрической системе. Траектории небесных тел не укладывались в круговые орбиты, а другие кривые не отвечали эстетическим вкусам греков. Клавдий Птоломей заметил, что Солнце обращается не столько вокруг Земли, сколько вокруг точки рядом с нею. Позднее это служило косвенным указанием на место расположения бога, сотворившего все сущее и любующегося им. Для того, чтобы теория не расходилась с практикой, поднаторевшие в геометрии эллины придумали эпициклы: так, задолго до рядов Фурье, возник метод последовательных приближений. Ныне им пользуются всякий раз, когда природа сигнала непонятна, не забывая поругивать древних за их щепетильность, ибо эллипс был им знаком.

Ведущая скрипка в космогонических учениях принадлежит Пифагору. Изучая резонансные явления, он обнаружил, что гармонические созвучия рождают струны, длины которых дают целые отношения. Это лишний раз подтверждало величие теории числа, построенной на процедуре деления. Понятие красоты сопричастно божественному вдохновению. Для того, чтобы постичь законы Вселенной, человек должен подняться от арифметики и геометрии к музыке и астрономии. Сложился "квадривиум", первая концепция образования, которую мы находим у Платона, ученика Сократа. Предполагалось, что планеты в кружении издают гармоничные созвучия, иначе небеса уподобились бы иррациональной Земле. Парадоксально, но факт, что поиски музыки небесных сфер вывели Кеплера и Ньютона на закон всемирного тяготения и теоретическую механику.

МЕХАНИЧЕСКИЕ МОДЕЛИ

На первом месте среди создателей механики стоит Архимед. Он родился в 287 г. до н. э. в Сицилии, в городе Сиракузах. Образование получил в Александрии, научная переписка связывала его с Эратосфеном. В покровительстве Архимед не нуждался, он был родственником царя Гиерона. Когда римляне осадили Сиракузы, они столкнулись с дьявольской изобретательностью этого неординарного ума. Предоставим слово Плутарху.

"При двойной атаке римлян Сиракузы онемели, поражённые ужасом. Что они могли противопоставить таким силам, такой могущественной рати? Архимед пустил в ход свои машины. Сухопутная армия была поражена градом метательных снарядов и громадных камней, бросаемых с великою стремительностью. Ничто не могло противостать их удару, они всё низвергали пред собою и вносили смятение в ряды. Что касается флота - то вдруг с высоты стен брёвна опускались, вследствие своего веса и приданной скорости, на суда и топили их. То железные когти и клювы захватывали суда, подымали их на воздух носом вверх, кормою вниз, и потом погружали в воду. А то суда приводились во вращение и, кружась, попадали на подводные камни и утёсы у подножья стен. Большая часть находившихся на судах погибала под ударом. Всякую минуту видели какое-нибудь судно поднятым в воздухе над морем. Страшное зрелище! Судно поворачивается из стороны в сторону, люди валятся, как бы пускаемые из пращи. Опустошённое судно или разбивается о стены, или погружается в море, будучи выпушено машиною.

Марцелл придвинул на большом помосте машину, называвшуюся самбук, по сходству с музыкальным инструментом этого имени. Когда она приближалась к стене и была ещё довольно далеко, Архимед пустил в неё камень весом в десять талантов, затем другой, третий. Камни, как бурею несомые, попадали в машину, ударялись в помост и разбивали его. Марцелл, не зная, что делать, поспешил увести флот и дал приказ войску на суше отступить. Был собран совет; порешили, если будет можно, ночью подойти под самые стены. Машины Архимеда с их огромною силою будут - думали - бросать снаряды так, что они пролетят над головами осаждающих, не попадая в них. Но Архимед давно заготовил приспособления на этот случай. Он расположил и такие машины, которых действие сопряжено было с расстоянием и которые почти без перерыва выбрасывали короткие копья. В стенах сделаны были многие дыры, чрез которые действовали на близком расстоянии скорпионы, невидимые неприятелем.

Достигнув стен, римляне воображали себя в безопасности, но они были под ударами. Камни падали на них сверху, стены - отовсюду пускали в них копья. Они, было, удалились, но машины слали новые метательные снаряды и поражали отступающих. Много погибло, суда сталкивались между собою, и осаждаемым причинить какой-либо вред было нельзя. Большая часть машин Архимеда была за стенами. Невидимая рука бросала тысячи зол в римлян: они боролись с богами. Сам Марцелл ускользнул от опасности. Подсмеиваясь над своими инженерами, он говорил: "Не перестать ли нам воевать с этим геометром Бриарием, который принимает корабли наши за ковши для черпания воды, разбивает самбук и превосходит сторуких мифологических великанов, бросая столько копий за раз". Действительно, население Сиракуз было телом, а Архимед - душою, проводившей все машины в движение. Все другие орудия бездействовали: только его употреблялись и для нападения, и для защиты. Под конец страх римлян сделался так велик, что как только увидят конец верёвки, бревно над стенами, обращаются в бегство, крича: "ещё машина Архимеда против нас!"

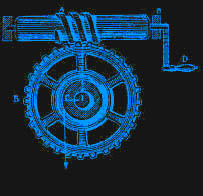
Циклопические пирамиды Египта свидетельствуют о знакомстве населявших его народов с клином и рычагом. Изображения чашечных весов и колодезного "журавля" (шадуф) встречаются в египетских папирусах [4]. Склонных к математическим изыскам александрийцев грубый рычаг мог заинтересовать законом пропорций, позволяющим дополнить популярные со времен Пифагора исследования рационального и иррационального наглядными механическими иллюстрациями. К теме рычага обращался не только прославленный купанием в ванне и битвами Архимед, но также астроном и геометр Евдокс. Позднее Папп Александриец (годы деятельности 305-284) подведет итог изучению свойств статических машин, указывая, что все сводится к пяти простым приспособлениям: ось с колесом (ворот), рычаг, полиспаст, клин и бесконечный винт, см. рис. 1.1.


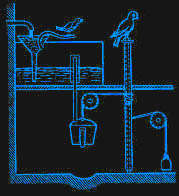
Рис 1.1. Бесконечный винт	Рис 1.2. Поющая птичка и сова

Водные процедуры Архимеда имели далеко идущие последствия. Сын брадобрея, искусный изобретатель Ктезибий, жил во II веке до н. э.. Он изготовил водяные часы с указателем, водяной орган, а также пожарную машину. Его ученик, Герон Александрийский, построил реактивную паровую "мельницу". Исследуя сифоны, он набрел на идею водного компаратора. Устройство прибора изображено на рис. 1.2., передающем детали игрушки "поющая птичка". Сифон представляет собой трубку, которая вставлена в дно кастрюльки. На трубку надета перевернутая пробирка. Кастрюлька медленно заполняется водой через воронку. Когда вода в пробирке достигает края трубки, возникает коленный ствол, каким часто пользуются шоферы. Кастрюлька опоражнивается. Приводимая механизмом в действие птичка свистит, когда сова на нее не смотрит.

КРИЗИС ФИЛОСОФИИ И МАТЕМАТИКИ

Зародившись в античной Греции, теория числа превратилась во всеми признаваемое ристалище, на котором испытывали свои силы сильнейшие математики. При делении яблока между едоками на доли нельзя получить иррациональное количество вещества. Греки были поражены изобретением геометрической машины, которая без натуги производила числа, не равные отношениям двух целых величин. Этот парадокс казался им родственником апорий Зенона. Отвергнув движение как фикцию, греки вполне последовательно вывели иррациональность за пределы понятия "число". В дальнейшем в Европе будет изготовлено много других "числоделательных" машин. Поиск корней полиномов увенчался открытием, появились алгебраические числа. Потом заявили о себе числа трансцендентные. Разрастающееся древо познания выбрасывало все новые и новые побеги.

В начале XIX века сортировать числа принялся сын садовода, Карл Фридрих Гаусс, переняв привычки селекционера у трудолюбивого отца. Своими работами он прославил Геттингенский университет, ставший с тех пор центром притяжения для математиков. Примерно в те же годы Эварист Галуа создал необычную арифметику над конечным набором элементов. Его таблица умножения четырех "чисел", содержащая в клетках только сомножители, производит неизгладимое эстетическое впечатление. В общем, алгебраисты в смелости поисков не уступали основоположникам неевклидовой геометрии. Уильям Гамильтон понял, что в угоду сложности суперкомплексного числа, кватерниона, придется пожертвовать коммутативным законом арифметики AB=BA. Он отсек одну ветвь, Давид Гильберт принялся за другие: данные им бледными едва различимыми красками трансфинитные абстракции бесполезно увеличивать, от суммирования они не возрастают, по определению A=A+1.

Каждая новая математическая машина отличалась присущими одной ей деталями. Следует ли их особенности складывать в одну кучку, и если да, то есть ли смысл говорить о пределах мыслимой Вселенной? Проблемы трисекции угла, удвоения куба, квадратуры круга волновали умы не одно столетие. Оказалось, что на ряд простых вопросов в геометрии нельзя получить ответы построениями при помощи циркуля и линейки. Абель, исследуя полиномы, указал на недостаточную разрешающую силу привычных арифметических операций. Если мы ограничиваем себя в средствах, вправе ли мы считать задачи неразрешимыми, и, наоборот, если наши возможности беспредельны, то в чем состоит содержание наших проблем? Конечно, чтобы достичь чего-либо, надо разумно ограничиться. Беда рассудку, когда граница разумного все время переносится.

"Мнимые числа, - писал в 1702 г. Готфрид фон Лейбниц, - это поразительный полет духа божьего; это почти амфибии, находящиеся где-то между бытием и небытием". Трудно подыскать, пожалуй, лучшее свидетельство опиумного действия плодов древа познания. Если мнимые числа - амфибии, то трансфинитные, уж точно, не более чем дымка от числа. Даже флюксии Ньютона заслужили более телесное прозвище "привидений". Леопольд Кронекер, вторя древним, считал, что целые числа суть творения божьи, а все остальные виды чисел - результат человеческой изобретательности. О том, какому пристальному досмотру подверглись божьи посланцы, свидетельствует определение положительных целых чисел, данное итальянцем Джузеппе Пеано:

"1 есть положительное целое число; за каждым положительным целым числом следует ровно одно и только одно положительное целое число; ни за каким положительным целым числом не следует 1; за разными положительными целыми числами следуют разные положительные целые числа; пусть некое утверждение выполняется для числа 1, и пусть всякий раз, как это происходит для некоторого положительного целого числа, оно выполняется и для следующего за ним числа, тогда это утверждение распространяется и на все положительные целые числа."

Стремясь прикрыть уязвимые места математики броней безупречных аксиом, К. Вейерштрасс, Р. Дедекинд и Г. Кантор тремя различными способами подошли к определению числа. Накопленный ими опыт лишний раз показал, что мыслимые вселенные не стремятся слиться и объяснить одну единственную, нашу. Их узор напоминает неплотно пригнанные чешуйки рыбы. При критическом обозрении между пластинами всегда обнаруживается досадный зазор. Исследования породили новые парадоксы. Выпас стада математических созданий только прибавил хлопот. Говоря языком биологии, проявили себя генетическая несовместимость и отторжение тканей, запахло всеобъемлющим кризисом математики.

Приблизимся к пугающему коллапсу с безопасной стороны. Задолго до эры книгопечатания природа изобрела свой печатный станок, репродуцируя ДНК. Кино, телевидение и радио - лишь слабое ему подражание и продолжение той же тенденции. Мощное информационное поле развивает и воспитывает людей. Человек в нем играет разве что роль электрона. На деле, неясно еще, кто кого создает и направляет, мы поле, или поле нас. Претворяя витающие в воздухе идеи в реальность, мы материализуем накопленный полем потенциал. Как это ни парадоксально, но мыслимые миры при всей их множественности - часть окружающей нас действительности, такая же, как земля под ногами и звезды над головой.

КРИЗИС ФИЛОСОФИИ И МАТЕМАТИКИ

ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ

Функциональный анализ изучает абстрактные бесконечномерные пространства и их отображения, преимущественно линейные, и то и другое может быть линейным.

Не секрет, что функциональный анализ, сколь бы много его ни абстрагировали, возник, изначально вокруг относительно простой идеи подобия интегрального уравнения системе линейных алгебраических уравнений (которая и получается из него при дескритизации). Соответственно, в бесконечномерной области возникают некие аналоги обратных операторов, матричной резольвенты, собственных значений.

При достаточно широком уже освещении матричного анализа в имеющейся литературе, проще назвать те отличия, которые несет в себе бесконечномерный случай, чем заняться буквоедским его изложением. Настоящая беда функционального анализа - это отсуствие достаточно простых поверхностных обзоров, которые бы дали перспективу этой дисциплины, потому что в ней много сборных уточняющих обширные приложения частей.

На первый взгляд, что добавляется, это существенная разница в трактовке спектра. Теперь спектр и собственные значения - это не одно и то же, как у матрицы. К спектру относятся все нерегулярные значения d операторной резольвенты А-dЕ, не все из них соответствуют собственным значениям Аx=dx. Дело в том, что обратный оператор может быть определен не на всем пространстве, это более широкая ситуация. Спектр может быть непрерывным. В ряде случаев точечный спектр сгущается, имеют место предельные точки.

Не совсем ясно, насколько это интересно - то, что касается собственно спектра, поскольку задача на собственные значения обособляется, тем самым.

Так, ограниченный в L2[a,b] и с виду безобидный оператор умножения x(t) на линейную функцию tx(t) не имеет в L2[a,b] собственных "векторов". При том, что их легко можно построить как дельта функции - напрашивающееся при аналогии с диагональными матрицами очевидное обобщение.

Хороший пример, это динамические системы. Им отвечает интегральный оператор свертки, или, как его еще называют, оператор Вольтерра. Собственных значений этот оператор не имеет, поскольку выходной сигнал динамической системы не повторяет входного. Рассмотрим импульсную весовую функцию системы. Ее можно считать "почти нулевой" (пренебрежимо малой) в сравнении с входным дельта-импульсом с его бесконечной амплитудой, то есть - в сравнении с почти "собственным вектором" при нулевом собственном значении.

В конечномерном случае почти собственных векторов не бывает, так как дельта-функция - полезная абстракция, порожденная интегральным исчислением.

Нуль в таком случае, это точка спектра, и все остальные особые точки (если они есть) в практически важных случаях к ней стремятся. Корневые "жордановы векторы" при этом строятся тривиально - как итерационно пересчитываемы реакции от любого полностью возбуждающего систему сигнала. Так как жорданова цепочка здесь строится бесконечно, от старшего вектора к младшему, до несуществующего "собственного вектора" дело никогда не доходит - неважно, что его нет. На последнее обстоятельство досадно редко указывают, хотя в этом видится общность к матрицам.

Наиболее полно проблема собственных значений разработана для случая линейных операторов в гильбертовом пространстве. Пусть А - ограниченный линейный оператор в гильбертовом пространстве H. Число d называется регулярной точкой оператора А, если обратный оператор (А-dЕ)-1 существует, ограничен и определён на всём пространстве. Остальные (не регулярные) значения d называется спектром оператора А. Между прочим, в примере с tx(t) ничто не мешает видеть в t диагональ некой бесконечномерной матрицы, и собственные значения (при дельта функциях в качестве собственных векторов), следовательно, размежевание непрерывного спектра и якобы дискретных собственных значений - от лукавого. Не ограничивайте множества - и получите более легкую аналогию. Течение мысли (нам уже неизвестной), возможно, когда то отбросило это, а забвение "ошибочных" ходов - не самое лучшее, для любой науки. Итак, спектру и собственным значениям (которые теперь не одно и то же), собственным и присоединенным (жордановым) векторам в бесконечномерном случае удается найти несколько спорные, но аналогии.

Большое значение в функциональном анализе придается понятиям, наследующим свойствам итерационных последовательностей. В частности, полноте пространств. Если не гнаться за более точными определениями, то полнота подразумевает сходимость итераций к элементам пространства. Для оценки сходимости берется норма разности двух соседних точек, она должна убывать.

Если отбрасывать лишние совершенно ненужные при поверхностном обозрении детали, то при построении функционального анализа из геометрии древних греков берутся такие понятия, как длина вектора и ортогональность векторов, известные подоплеки построения банаховых и гильбертовых пространств соответственно.

Банаховы пространства в какой то мере ближе к интерпретации матриц, у которых есть норма - этот аналог длины - и матрицы, к тому же, дают весьма популярную аналогию линейного преобразования, этой второй составляющей функционального анализа. Гильбертово бесконечномерное пространство, обыгрывающее понятие ортогональности, и есть наиболее близкое обобщение пространства векторов Декарта. В теории встречается термин сепарабельность - когда на абстрактном множестве есть всюду плотное счетное множество. Сторона дела, нужная тогда, когда в бесконечномерном пространстве мы строим счетный базис. Мощности любых двух полных ортонормированных систем в сепарабельном пространстве одинаковы. Такого сорта формулировки - дань бесконечности.

Далее двигаться уже более легко. В линейных пространствах в построение одних элементов из других вовлекаются числа, вещественные или комплексные. Если сумма элементов с масштабными множителями в виде чисел имеет смысл элемента же, то пространство линейно, поскольку обретает содержание термин быть линейно зависимым (выражаться через такие комбинации).

По контексту, существуют линейно независимые "векторы". Все становится более или менее привычным. В полных линейных пространствах элементы, рассматриваемые как возможно базисные, можно проредить, удалить линейно зависимые, а это и есть, собственно, построение базиса. Базис, это отсев существенного в ущерб несущественному. Мы почти дотянулись до первого нужного нам пространства - банахова.

Банахово пространство - это полное линейное нормированное пространство. Нормированное означает наличие обобщенной длины - нормы элемента (т.е. умение ее посчитать). В ряде случаев (тут рассуждение обретает свободу) можно согласовывать меру расстояния между элементами и их величины, вводя первое как величину разности элементов, коль скоро в линейном пространстве можно оперировать разностями.

Теория двигается по накатанному рецепту. Потрудившись, основоположники выписали основные свойства хорошо известного скалярного произведения векторов. Если для элементов бесконечномерного линейного нормированного пространства можно построить функцию, обладающую свойствами скалярного произведения, то гильбертово пространство, при всей его абстрактности, построено.

Скалярное произведение ортогональных векторов равно нулю. В гильбертовом пространстве можно вводить и иные понятия из геометрии, такие как проекция элемента на произвольное подпространство. И оператор проецирования. Линейный, обобщающий понятие матрицы, с помощью которых строятся операции преобразования векторов.

Линейные операторы в гильбертовых пространствах, таким образим, просто естественное следствие структуры пространств. Тут появляется и получает звучание также унитарный оператор, отображающий гильбертово пространство в себя и сохраняющий скалярное произведение. На этой стадии аксиоматическое построение теории наследут понятия, привычные для конечномерных пространств.

Для характеристики операторов вводят понятия их непрерывности (ограниченности по норме) и вполне непрерывности (компактности). Компактность и предкомпактность - это прежде всего свойство пространств.

Суть компактности - в исчерпываемости некого бесконечномерного пространства конечномерным приближением с любой наперед заданной точностью. Таким образом существуют две бесконечности - актуальная, это когда приближения эффективны в начале бесконечных по существу итераций (или линейных комбинаций), и не очень актуальная, это когда возможность приближения отодвинута в бесконечно достигаемый же "конец".

Для иллюстраций понятия компактность привлекается теория числа - еще один источник, питающий функциональный анализ. Так, бесконечная числовая прямая в этой терминологии некомпактна, поскольку на ней есть натуральные числа, приближать их чем-то конечномерным в принципе нельзя. Если множество ограниченно и замкнуто, т.е. содержит все свои предельные точки, см. дальше, то оно компактно (теорема Больцано-Веершрасса).

Если мы покидаем теорию числа и переходим к функциям, то на этот счет есть сходная теорема Арцела. Пусть множество функций равномерно ограничено (модуль функции не превосходит порога) и функции равностепенно непрерывны (вычисленный в дискретных точках наклон кривой, некое подобие производной, ограничен). Тогда множество компактно.

Линейный оператор, переводящий ограниченное множество, допустим, бесконечномерный шар, в компактное (или, более строго, в предкомпактное, если не брать в расчет предельные точки), тоже называется компактным или вполне непрерывным.

Такой оператор наследует свойства конечномерного оператора в том смысле, что всегда может быть приближен им. Если приближается множество на выходе, то и оператор может быть приближен элементарным огрублением выхода. Вот основная мысль функционального анализа. Корни этой дисциплины - еще в составных моделях планетарного движения древних и в рядах Фурье.

У непрерывного оператора можно посчитать конечное значение норм входного и выходного элементов, максимальное значение этого отношения на всем множестве определения дает согласованную норму самого этого оператора. Грубо говоря, это максимальный "коэффициент усиления" преобразования. Поэтому такой оператор называют еще ограниченным. Непрерывность - достаточно естественное свойство отображений, интуитивно понятное, скажем, по отображению 2x.

Поскольку есть норма, такие операторы сами по себе образуют банахово пространство относительно обычных алгебраических операций. Ведь и матрицы в чем то подобны векторам, их можно преобразовывать. Это видимое усложнение однако - не более чем собирательство фактов и дефиниций. Здесь нет новой теории, а начинается спекуляция. Оставим ее.

Из предыдущего следует, что одной лишь непрерывности (как у тождественного оператора) нам мало, нужно, чтобы оператор был вполне непрерывным (компактным), то есть, упрощал выходное множество до возможности его конечномерного описания с любой степенью точности (до компактного). Интегральные операторы - как раз подходящий материал для этого.

Обратный оператор, естественно, не наследует у вполне непрерывного оператора это качество. Вход и выход слишком разные. И тождественный оператор - некомпактен. В этих условиях строить решение некого подобия системы линейных алгебраических уравнений - возможно, если еще более сужать рассматриваемые множества. Это реально, но в большинстве практически важных случаев не требуется, как игнорируются, например, недоопределенности (в классическом анализе) дельта функции. Тем не менее, обратное отображение, естественно, вводится и используется в определении гомеоморфизма.

Далее в ход вступают привычные при конечномерном анализе инструменты. Оператор А* называется сопряжённым к А, если скалярное произведение (Ax,у)=(х,А*у) для всех х и у из Н. Оператор А называется самосопряжённым, если А=А*, и унитарным, если А*=А-1. Добавляется, что самосопряжённые и унитарные операторы представляют собой важнейшие и наиболее полно изученные классы линейных операторов в гильбертовом пространстве. Их теория является обобщением теории самосопряжённых и унитарных линейных преобразований n-мерного евклидова пространства.

Самосопряжённый вполне непрерывный оператор А имеет хотя бы одно собственное значение, причём в Н можно выбрать полную ортогональную систему элементов, состоящую из собственных функций оператора А.

Отсылки к морфизмам (подобиям) популярны в любой науке. Гомеоморфизм - следующее, помимо компактности, основное понятие топологии. Две фигуры (точнее, два топологических пространства) называются гомеоморфными, если существует взаимно однозначное непрерывное отображение любой из них на другую, для которого обратное отображение тоже непрерывно, при этом само отображение называется гомеоморфизмом. Например, любой круг гомеоморфен любому квадрату, любые два отрезка гомеоморфны, но отрезок не гомеоморфен ни окружности, ни прямой. Прямая гомеоморфна любому интервалу (то есть отрезку с удалёнными концами). Понятийный аппарат охватывает терминологией и сходные свойства преобразований, например, изоморфизм. Абстрагируясь от свойств конкретных пространств, мы можем получить две совершенно сходные алгебраические конструкции и элементарный принцип экономии состоит в том, чтобы изучать их как одну - поскольку вследствие их изоморфизма, так это называют, они различимы лишь на уровне их приложений.

Вполне непрерывные операторы нужны там, где они уместны. Преимущественно это интегральные операторы. Теория разрешимости линейных уравнений исторически строилась для интегральных уравнений Фредгольма 2-го рода вида x-Ax=у. В такой постановке проблема явно имеет пересечения с теорией собственных значений (для однородных уравнений). Весьма общие теоремы о разложении функций в ряды Фурье доказал Д. Гильберт (1904) с помощью теории линейных интегральных уравнений.

Можно было бы сказать, следовательно, что функциональный анализ - это теория вполне-непрерывных операторов. Операторов почти конечномерных. Так можно было бы сказать, если бы не было дифференциальных операторов.

Важнейшим классом неограниченных линейных операторов в гильбертовом пространстве были и остаются дифференциальные операторы. И вот почему.

Многие задачи математической физики, в частности теории колебаний, приводят к задаче о разыскании собственных функций и собственных значений различных дифференциальных операторов. Например, цилиндрические функции, Лежандра многочлены и т.д. представляют собой не что иное, как собственные функции определённых дифференциальных операторов.

Задача Штурма-Лиувилля. Задача о нахождении отличных от нуля решений дифференциального уравнения вида -[p(x)y']'+q(x)y=dy, удовлетворяющих граничным условиям вида A1y(a)+B1y'(a)=0, А2у(b)+B2y'(b)=0 (т.н. собственных функций), а также о нахождении значений параметра d (собственных значений), при которых существуют такие решения. При некоторых условиях на коэффициенты р(х), q(x) задачу можно свести к рассмотрению аналогичной задачи для уравнения вида -y"+q(x)y=dy. Была впервые (1837-41) исследована Ж. Лиувиллем и Ж.Ш.Ф. Штурмом. Решение некоторых видов уравнений математической физики методом Фурье приводит к задаче Штурма-Лиувилля.

Например, к ней приводит задача о колебаниях однородной струны, закрепленной на концах, для уравнения -у"=dу с граничными условиями y(0)=y(p)=0. В этом случае существует бесконечная последовательность собственных значений, которым соответствуют собственные функции sin(nx), образующие на отрезке [0,p] полную ортогональную систему функций. Аналогично обстоит дело и в общем случае, возникающем, например, при изучении распространения тепла в неоднородном стержне и т.д. И здесь, если функция q(x) в уравнении непрерывна и действительна на отрезке [a,b], a коэффициенты граничных условий - действительные числа, существует возрастающая последовательность действительных собственных значений, стремящаяся к бесконечности, причём каждому из собственному значению соответствует определённая с точностью до постоянного множителя собственная функция, имеющая n нулей. Полнота такой системы функций была доказана В. А. Стекловым в 1896.

Шутка. Математик компактен. Потому что он ограничен и замкнут.